RANGKUMAN MATEMATIKA KELAS 9 SEMESTER 1 KURIKULUM 2013
Bilangan berpangkat dan bentuk Akar
(BAB I)
Bilangan berpangkat
pangkat suatu bilangan adalah perkalian suatu bilangan secara berulang dengan bilangan itu sendiri
Bentuk : An = a x a x … x a = b
a : bilangan pokok
n : pangkat
b : hasil dari perpangkatan
Rumus
Am x an = am+n
Am : an = am/ an = am-n
(am)n = a mxn
(axb)m = am x bm
(a.b)n = an/bn
A0=1
Contoh :
-24 = -2 x -2 x -2 x -2 = 16
-(2)4 = -(2.2.2.2)= -16
(2/3)3 = 2/3 x 2/3 x 2/3 = 8/27
Nilai operasi perpangkatan
Contoh :
Akar
Pola Barisan dan Deret
(BAB II)
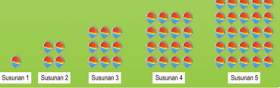
pola bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan. Dalam matematika dikenal beberapa jenis pola bilangan antara lain:
- Pola bilangan ganjil adalah 1,3,5,7. Rumus urutan ke-n adalah 2n-1 dan jumlah bilangan n adalah n2.
- Pola bilangan genap adalah 2,4,6,8. Rumus urutan ke-n adalah 2n dan jumlah dari n bilangan genap adalah n(n + 1)
- Pola bilangan segitiga adalah 1,3,6,10. Rumus urutan ke-n n(n+1)/2
- Pola bilang persegi adalah 1,4,9,16. Rumus urutan ke-n adalah n2
- Pola bilangan persegi panjang 2,6,12,20. Rumus urutan ke-n adalah n(n+1)
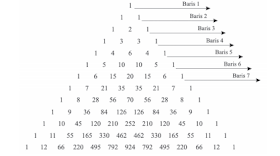
- Setiga pascal. Rumus jumlah bilangan baris ke-n adalah 2n-1
Suku ke-n suatu barisan bilangan
Rumus suku ke-n adalah Un= a+ (n-1)b
a = U1 : suku pertama
Un = Suku ke- n
n : banyak suku
b= Un-Un-1= beda antara 2 suku berurutan
Suku tengah deret Aritmatika
Ut = U1 + Un/2
Ut : suku tengah
U1 : Suku pertama
Un : suku ke-n
Jumlah n suku pertama deret Aritmatika
Sn= 1/2 x n ( U1 + Un)
atau
Sn= 1/2 x n ( 2U1 +(n-1)b)
Deret geometri
deret geometri adalah deret dengan rasio antar 2 suku yang berurutan selalu tetap.
Jumlah n suku pertama deret geometri
Sn = U1 (rn-1)/ r-1
Sn : Jumlah suku pertama
U1 : Suku pertama
r : rasio
n : banyak suku
Perbandingan bertingkat
(BAB III)
perbandingan bertingkat adalah membandingkan 2 nilai atau lebih dari suatu besaran yang sejenis dan dinyatakan dengan cara sederhana. Persentase adalah pecahan dengan penyebut
contoh perbandingan bertingkat :
Harga 1 kodi pena adalah 32.000. Harga 1 lusin pena adalah
1 kodi = 20 buah
1 Lusin = 12 buah
20 buah pena = 32.000
12 buah pena = x
20/12 = 32.000/x
20 x= 384.000
x = 384.000/ 20
x = Rp 19.200
Sebuah proyek direncanakan dapat diselesaikan dalam waktu 9 bulan oleh 140 karyawan. Jika proyek tersebut dipercepat penyelesaiannya maka agar dapat selesai dalam waktu 7 bulan jumlah karyawan yang harus ditambahkan sebanyak?
DIK :
140 karyawan = 9 bulan
x = 7 bulan
140/x = 7/9
7x = 1260
x = 1260/7
x = 180
180- 140 = 40 tambahan karyawan
Persentase
(BAB IV)
1. Menentukan persentase untung dan rugi terhadap pembelian
keuntungan/ x 100 %
harga beli
persentase rugi dari harga beli
Kerugian / x 100%
harga beli
2. Menghitung harga jual dan beli
pedangang dalam kondisi untung :
J=B + BxU/100
Pedangang dalam kondisi rugi :
J = B - B x R/100
Untuk menghitung harga beli
pedagang dalam kondisi untung
B= 100j/ 100 +U
pedagang dalam kondisi rugi
B= 100J/100- R
Sumber : http://vven27.blogspot.com/2016/02/rangkuman-matematika-kelas-9-semester-1.html?m=1

















0 komentar: